B-Trees: Warum jede Datenbank sie verwendet
Um 3 Uhr morgens crashte mein B-Tree bei genau 16.777.215 Einträgen. Im MySQL-Quellcode fand ich denselben Off-by-One Bug, den sie Jahre zuvor behoben hatten. Dieser Deep-Dive erklärt, warum B-Trees seit über 50 Jahren die Datenbank-Indexierung dominieren—und wann man sie nicht verwenden sollte.
B-Trees: Warum jede Datenbank sie verwendet
Verstehen Sie die Datenstruktur, die Datenbanken auf Festplatten schnell macht.
Vor drei Jahren, 3 Uhr morgens, arbeitete ich mich durch das Kapitel 2 von "Database Internals" von Alex Petrov.
Es erklärt, warum binäre Suchbäume auf Festplatten versagen. Warum niedriger Fanout die Performance zerstört und warum B-Trees gewonnen haben. Ich dachte: "Ich implementiere das in Python, um es wirklich zu verstehen."
16.777.215 Einträge später stürzte mein Baum ab. 2^24 minus 1. Der rechte Kind-Zeiger wurde überschrieben, was den gesamten Baum beschädigte. Jedes einzelne Mal.
Ich war eine Taste davon entfernt, alles zu löschen und einfach eine Hash Map zu verwenden.
Dann, mehr aus Trotz als aus Hoffnung, öffnete ich den InnoDB-Quellcode.
storage/innobase/btr/btr0cur.cc:4083
Ein Kommentar sprang mir ins Auge:
"btr_page_split_and_insert() in btr_cur_pessimistic_insert() invokes..."
Pessimistic insert. Das ist der Code-Pfad, wenn ein Knoten zu voll ist. Wenn optimistic insert fehlschlägt und wann man splitten MUSS.
Ich folgte der Funktion zu btr0btr.cc. Hunderte Zeilen C-Code. Split-Bedingungen. Overflow-Guards. Und—eine Off-by-One-Prüfung, die ich nicht hatte.
Ich scrollte durch meinen Python-Code:
Im Buch auf der Seite 263 stand: "If the node can hold up to N key-value pairs, and inserting one more brings it OVER its maximum capacity N."
ÜBER. Nicht gleich. Über.
Da war es. Genau derselbe Bug, den die Entwickler vor Jahren behoben hatten. Ich hatte ihn unwissentlich reproduziert.
In diesem Moment verstand ich, warum jede Datenbank seit 50 Jahren auf B+-Trees vertraut—und nie etwas anderes für Indizes verwendet hat.
Das ist die Geschichte dieses Aha-Moments.
Ihre Datenbank hat 10 Millionen Benutzerdatensätze. Sie fragen nach einem Benutzer per ID. Die Datenbank liefert das Ergebnis in 3 Millisekunden. Wie?
Wenn die Datenbank alle 10 Millionen Datensätze sequentiell scannen würde, würde es Sekunden, vielleicht Minuten dauern. Aber Datenbanken scannen nicht. Sie verwenden einen Index—und dieser Index ist fast sicher ein B-Tree.
Jedes grosse Datenbanksystem verwendet B-Trees: MySQL InnoDB, PostgreSQL, SQLite, MongoDBs WiredTiger Storage Engine, Oracle Database, Microsoft SQL Server. Das ist kein Zufall. B-Trees lösen ein fundamentales Problem: wie man Daten auf Festplatten effizient findet, wenn Festplattenzugriffe tausendmal langsamer sind als Speicherzugriffe.
Das ist die Geschichte, warum binäre Suchbäume auf Festplatten versagen, wie B-Trees dieses Problem lösen, und warum wir sie nach über 50 Jahren immer noch verwenden.
Interesse an Shop Performance-Optimierung?
Kostenloses Erstgespräch & Bedarfsabklärung
Das Problem: Binäre Suchbäume auf Festplatten
Beginnen wir mit dem, was nicht funktioniert: binäre Suchbäume (BSTs) auf Festplatten.
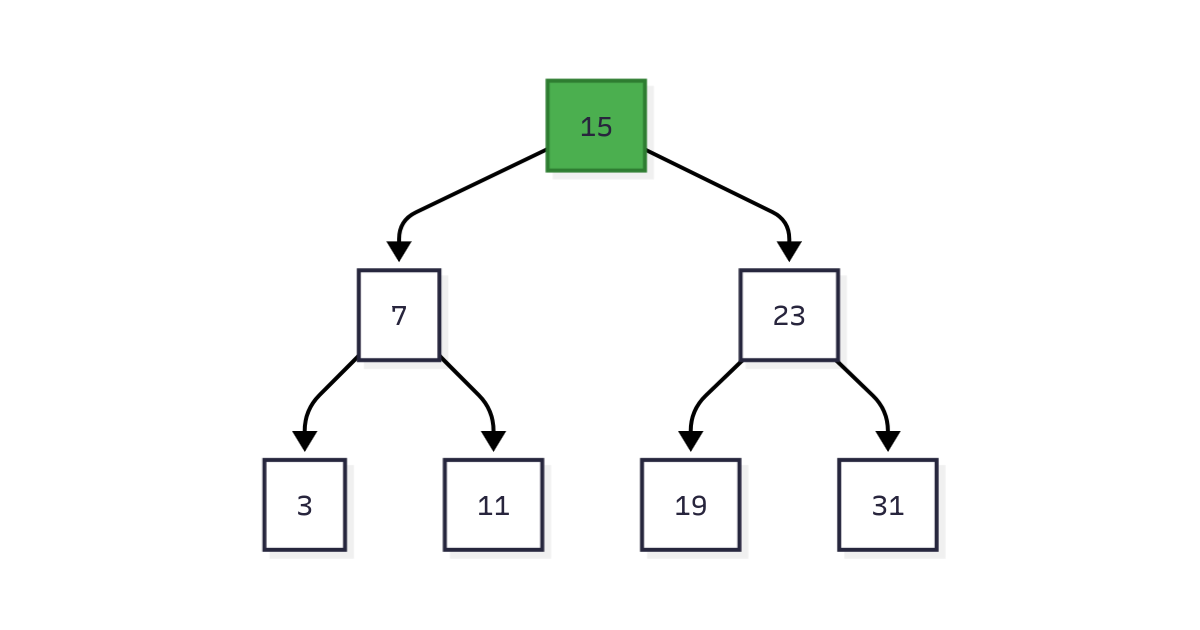
Im Arbeitsspeicher sind binäre Suchbäume ausgezeichnet. Jeder Knoten speichert einen Schlüssel und hat zwei Kinder (links und rechts). Schlüssel im linken Teilbaum sind kleiner, Schlüssel im rechten Teilbaum sind grösser. Das Finden eines Schlüssels benötigt O(log₂ n) Vergleiche.
Abbildung 1: Binärer Suchbaum mit 7 Knoten. Das Finden von Schlüssel 11 benötigt 3 Vergleiche: 15 → 7 → 11.
Für 1 Million Datensätze hat ein balancierter BST die Höhe log₂(1.000.000) ≈ 20. Das sind 20 Vergleiche, um jeden Datensatz zu finden.
Im Arbeitsspeicher ist das schnell. Jeder Vergleich ist eine Zeiger-Dereferenzierung (~0,0001 Millisekunden auf modernen CPUs). Gesamte Suchzeit: 0,002 ms.
Auf Festplatten ist das katastrophal. Hier ist der Grund:
Festplatten-I/O ist teuer
Die kleinste Einheit des Festplattenzugriffs ist ein Block (typischerweise 4 KB bis 16 KB). Um ein einzelnes Byte von der Festplatte zu lesen, muss man den gesamten Block lesen, der es enthält.
Festplatten-Zugriffszeiten:
| Speichertyp | Random Access Latenz | Sequentielle Lesegeschwindigkeit |
|---|---|---|
| HDD (Festplatte) | 10 ms | 100 MB/s |
| SATA SSD | 0,1 ms | 500 MB/s |
| NVMe SSD | 0,02 ms | 3.000 MB/s |
| RAM | 0,0001 ms | 20.000 MB/s |
Festplatten sind 100-100.000x langsamer als RAM.
Das Binärbaum-Desaster
Mit einem BST auf Festplatte wird jeder Knoten in einem separaten Festplattenblock gespeichert. Das Traversieren von Eltern zu Kind erfordert eine Festplatten-Suche.
Für 1 Million Datensätze:
- Höhe: 20 Knoten
- Festplatten-Seeks: 20
- Zeit auf HDD: 20 × 10 ms = 200 Millisekunden
- Zeit auf SSD: 20 × 0,1 ms = 2 Millisekunden
Das ist akzeptabel für SSDs, aber schrecklich für HDDs. Und es wird schlimmer, je grösser der Baum wird.
Für 1 Milliarde Datensätze:
- Höhe: 30 Knoten
- Zeit auf HDD: 30 × 10 ms = 300 Millisekunden
- Zeit auf SSD: 30 × 0,1 ms = 3 Millisekunden
Das fundamentale Problem: BST-Fanout ist zu niedrig (nur 2 Kinder pro Knoten). Wir brauchen mehr Kinder pro Knoten, um die Baumhöhe zu reduzieren.
Warum nicht einfach den Baum balancieren?
Man könnte denken: "Halt den Baum einfach balanciert!" Red-Black-Trees und AVL-Trees machen das.
Das Problem ist nicht nur die Baumhöhe—es sind die Wartungskosten. Balancieren erfordert das Rotieren von Knoten und das Aktualisieren von Zeigern. Im Arbeitsspeicher ist das günstig (ein paar Zeiger-Schreibvorgänge). Auf Festplatten ist es teuer:
- Knoten von Festplatte lesen (4 KB Block)
- Knoten im Speicher modifizieren
- Modifizierten Knoten zurück auf Festplatte schreiben (4 KB Block)
- Eltern-Zeiger aktualisieren (mehr Festplatten-I/O)
Für einen Baum mit häufigen Einfügungen und Löschungen zerstört ständiges Rebalancieren die Performance. Wir brauchen eine Datenstruktur, die:
- Hohen Fanout hat (viele Kinder pro Knoten) → reduziert Höhe
- Seltenes Rebalancieren erfordert → reduziert I/O-Overhead
Diese Datenstruktur ist der B-Tree.
Was ist ein B-Tree?
Ein B-Tree ist ein selbstbalancierender Baum, optimiert für Festplattenzugriff. Anstatt 2 Kinder pro Knoten (binärer Baum), hat ein B-Tree-Knoten Hunderte oder Tausende von Kindern.
Kernidee: Jeder B-Tree-Knoten passt in einen Festplattenblock (4 KB bis 16 KB). Da wir sowieso den ganzen Block lesen müssen, packen wir so viele Schlüssel wie möglich hinein.
B-Tree-Struktur
Ein B-Tree-Knoten speichert:
- N Schlüssel (sortiert)
- N + 1 Zeiger zu Kind-Knoten
Jeder Schlüssel fungiert als Separator: Schlüssel in child[i] sind kleiner als key[i], Schlüssel in child[i+1] sind grösser oder gleich key[i].
Abbildung 2: B-Tree mit Fanout ~100. Wurzel hat 2 Schlüssel und 3 Kinder. Interne Knoten haben 4 Schlüssel und 5 Kinder. Blattknoten enthalten die eigentlichen Daten.
B-Tree-Hierarchie
B-Trees haben drei Arten von Knoten:
Wurzel-Knoten: Die Spitze des Baums. Es gibt immer genau eine Wurzel.
Interne Knoten: Mittlere Schichten, die Suchen leiten. Sie speichern Separator-Schlüssel und Zeiger, aber keine eigentlichen Daten.
Blattknoten: Unterste Schicht, die die eigentlichen Daten enthält (Schlüssel-Wert-Paare). Alle Blätter sind auf der gleichen Tiefe.
Das ist ein B+-Tree, die häufigste Variante. B+-Trees speichern Daten nur in Blättern, während B-Trees Daten auch in internen Knoten speichern können. Jede grosse Datenbank verwendet B+-Trees, nennt sie aber der Einfachheit halber "B-Trees".
Warum hoher Fanout wichtig ist
Binärbaum (Fanout = 2):
- 1 Million Datensätze → Höhe = 20
- 1 Milliarde Datensätze → Höhe = 30
B-Tree (Fanout = 100):
- 1 Million Datensätze → Höhe = 3 (weil 100³ = 1.000.000)
- 1 Milliarde Datensätze → Höhe = 5 (weil 100⁵ = 10.000.000.000)
B-Tree (Fanout = 1000):
- 1 Million Datensätze → Höhe = 2 (weil 1000² = 1.000.000)
- 1 Milliarde Datensätze → Höhe = 3 (weil 1000³ = 1.000.000.000)
| Fanout | 1M Records Höhe | 1B Records Höhe | Festplatten-Seeks (HDD) | Zeit (HDD) |
|---|---|---|---|---|
| 2 (BST) | 20 | 30 | 20 | 200 ms |
| 100 | 3 | 5 | 3 | 30 ms |
| 1000 | 2 | 3 | 2 | 20 ms |
Hoher Fanout = weniger Festplatten-Seeks = schnellere Abfragen.
B-Tree Lookup-Algorithmus
Das Finden eines Schlüssels in einem B-Tree ist eine Wurzel-zu-Blatt-Traversierung mit binärer Suche an jedem Knoten.
Algorithmus:
- Starte beim Wurzel-Knoten
- Binäre Suche der Schlüssel im aktuellen Knoten, um den Separator-Schlüsselbereich zu finden
- Folge dem entsprechenden Kind-Zeiger
- Wiederhole bis zum Blattknoten
- Im Blatt entweder den Schlüssel finden oder feststellen, dass er nicht existiert
Zeitkomplexität:
- Baumhöhe: O(log_fanout n)
- Binäre Suche pro Knoten: O(log₂ fanout)
- Total: O(log n)
Beispiel: Finde Schlüssel 72 in einem B-Tree mit Fanout 100 und 1 Million Datensätzen.
Funktionierende Implementierung in Python
Implementieren wir einen vereinfachten aber funktionalen B-Tree in Python.
Ausgabe:
Warum diese Implementierung funktioniert:
- Jeder Knoten speichert bis zu
order - 1Schlüssel - Die Split-Operation erhält die B-Tree-Invarianten
- Binäre Suche innerhalb der Knoten reduziert Vergleiche
- Die Baumhöhe bleibt logarithmisch
B-Tree Node Splits
Wenn Sie einen Schlüssel in einen vollen Blattknoten einfügen, muss der Knoten gesplittet werden.
Split-Algorithmus:
- Finde den Mittelpunkt des vollen Knotens
- Erstelle einen neuen Geschwisterknoten
- Verschiebe die Hälfte der Schlüssel zum neuen Knoten
- Befördere den mittleren Schlüssel zum Elternknoten
- Wenn der Elternknoten voll ist, splitte ihn rekursiv
Abbildung 3: Node Split beim Einfügen. Der volle Knoten wird am Mittelpunkt gesplittet, und der mittlere Schlüssel (30) wird zum Elternknoten befördert.
Wenn Splits zur Wurzel propagieren:
- Die Wurzel wird in zwei Knoten gesplittet
- Eine neue Wurzel wird mit einem Schlüssel erstellt (der beförderte Schlüssel von der alten Wurzel)
- Die Baumhöhe erhöht sich um 1
Das ist der einzige Weg, wie die Baumhöhe in einem B-Tree zunimmt. B-Trees wachsen nach oben von den Blättern, nicht nach unten von der Wurzel.
B-Tree Node Merges
Wenn Sie einen Schlüssel aus einem Knoten löschen und er zu leer wird (unter 50% Kapazität), wird er mit einem Geschwisterknoten zusammengeführt.
Merge-Algorithmus:
- Kopiere alle Schlüssel vom rechten Geschwister zum linken Geschwister
- Degradiere den Separator-Schlüssel vom Elternknoten in den zusammengeführten Knoten
- Entferne den rechten Geschwisterknoten
- Wenn der Elternknoten zu leer wird, führe ihn rekursiv zusammen
Abbildung 4: Node Merge beim Löschen. Wenn der rechte Knoten zu leer wird, wird er mit dem linken Knoten zusammengeführt, wobei der Separator-Schlüssel vom Elternknoten gezogen wird.
Wenn Merges zur Wurzel propagieren:
- Wenn die Wurzel nach einem Merge nur ein Kind hat, wird dieses Kind zur neuen Wurzel
- Die Baumhöhe verringert sich um 1
Splits und Merges halten den Baum balanciert. Alle Blattknoten bleiben auf der gleichen Tiefe, was konsistente Abfrage-Performance gewährleistet.
B-Tree Performance-Charakteristiken
Lookup-Komplexität
Zeitkomplexität: O(log n)
Für einen Baum mit n Schlüsseln und Fanout f:
- Baumhöhe: log_f(n)
- Binäre Suche pro Knoten: log₂(f)
- Totale Vergleiche: log_f(n) × log₂(f) = O(log n)
Festplatten-I/O: log_f(n) Festplattenlesevorgänge (einer pro Ebene)
Insert-Komplexität
Zeitkomplexität: O(log n)
- Lookup um Einfügepunkt zu finden: O(log n)
- Einfügen ins Blatt: O(f) um Schlüssel zu verschieben
- Split falls nötig: O(f) um Schlüssel zu verschieben
- Splits propagieren nach oben: O(log n) Ebenen im schlimmsten Fall
Festplatten-I/O: O(log n) Lesevorgänge + O(log n) Schreibvorgänge
Delete-Komplexität
Zeitkomplexität: O(log n)
- Lookup um Schlüssel zu finden: O(log n)
- Löschen aus Blatt: O(f) um Schlüssel zu verschieben
- Merge falls nötig: O(f) um Schlüssel zu verschieben
- Merges propagieren nach oben: O(log n) Ebenen im schlimmsten Fall
Festplatten-I/O: O(log n) Lesevorgänge + O(log n) Schreibvorgänge
Speicherkomplexität
Speicher: O(n)
Jeder Schlüssel wird einmal gespeichert. Interne Knoten fügen Overhead hinzu (Zeiger und Separator-Schlüssel), aber das sind typischerweise 10-20% der Datengrösse.
Belegung: Knoten sind typischerweise zu 50-90% gefüllt. Höherer Fanout verbessert die Speichereffizienz, weil der Zeiger-Overhead proportional kleiner wird.
B-Tree-Verwendung in der Praxis
Jede grosse Datenbank verwendet B-Trees (oder B+-Trees) für Indizes.
MySQL InnoDB
InnoDB verwendet B+-Trees für:
- Primary Key Index (Clustered Index): Speichert tatsächliche Zeilendaten in Blattknoten
- Secondary Indexes: Speichern Zeiger zum Primary Key in Blattknoten
InnoDB B-Tree-Konfiguration:
- Seitengrösse: 16 KB (Standard)
- Fanout: ~100-200 je nach Schlüsselgrösse
- Baumhöhe für 1 Million Zeilen: 3-4 Ebenen
Beispiel:
InnoDB Abfrage-Performance:
PostgreSQL
PostgreSQL verwendet B-Trees als Standard-Indextyp.
PostgreSQL B-Tree-Konfiguration:
- Seitengrösse: 8 KB (Standard)
- Fanout: ~50-100 je nach Schlüsselgrösse
- Unterstützt mehrere Indextypen (B-Tree, Hash, GiST, GIN, BRIN), aber B-Tree ist Standard
Beispiel:
SQLite
SQLite verwendet B-Trees sowohl für Tabellen als auch für Indizes.
SQLite B-Tree-Konfiguration:
- Seitengrösse: 4 KB (Standard, konfigurierbar bis 64 KB)
- Fanout: ~50-100
- Alle Daten werden in B-Trees gespeichert (kein separater Heap-Speicher)
Interessante Tatsache: SQLite nennt seine B-Tree-Implementierung aus historischen Gründen "r-tree", aber es ist tatsächlich ein B+-Tree.
MongoDB WiredTiger
MongoDBs WiredTiger Storage Engine verwendet B-Trees für Indizes.
WiredTiger B-Tree-Konfiguration:
- Interne Seitengrösse: 4 KB (Standard)
- Blatt-Seitengrösse: 32 KB (Standard)
- Fanout: ~100-200
- Unterstützt Präfix-Kompression um Fanout zu erhöhen
Beispiel:
Trade-offs und Limitierungen
B-Trees sind nicht perfekt. Hier haben sie Schwächen:
1. Write Amplification
Jedes Insert kann Splits bis zur Wurzel auslösen. Im schlimmsten Fall:
- 1 Schlüssel einfügen → Blatt splitten → Eltern splitten → Grosseltern splitten → Wurzel splitten
- Ein logischer Schreibvorgang wird zu 4+ physischen Schreibvorgängen
Beispiel: 1 Million Schlüssel mit häufigen Splits einfügen:
- Logische Schreibvorgänge: 1 Million
- Physische Schreibvorgänge (mit Splits): 2-3 Millionen
- Write Amplification: 2-3x
Alternative: LSM-Trees (Log-Structured Merge Trees), verwendet von RocksDB, Cassandra und LevelDB. LSM-Trees sammeln Schreibvorgänge im Speicher und schreiben sequentiell auf die Festplatte, wodurch In-Place-Updates vermieden werden.
2. Range Queries auf nicht-sequentiellen Schlüsseln
B-Trees sind für Range Queries auf dem indizierten Schlüssel optimiert, haben aber Schwierigkeiten mit Multi-Column Range Queries.
Beispiel:
Alternative: Mehrdimensionale Indizes wie R-Trees (für Geodaten) oder Hybrid-Indizes.
3. Speicher-Overhead für Caching
Um Festplatten-I/O zu vermeiden, cachen Datenbanken häufig genutzte B-Tree-Knoten im Speicher. Für eine grosse Datenbank:
- 1 Milliarde Datensätze
- Baumhöhe: 4 Ebenen
- Interne Knoten: ~1 Million
- Cache-Grösse: ~16 GB (um alle internen Knoten zu cachen)
Faustregel: Planen Sie 10-20% Ihrer Datenbankgrösse als RAM für B-Tree-Caches ein.
4. Fragmentierung über Zeit
Nach vielen Einfügungen und Löschungen können B-Tree-Knoten nur zu 50-60% gefüllt sein. Das verschwendet Speicherplatz und erhöht die Baumhöhe.
Lösung: Periodisches VACUUM (PostgreSQL) oder OPTIMIZE TABLE (MySQL) um B-Trees neu aufzubauen.
Beispiel:
5. Concurrency-Herausforderungen
B-Trees erfordern Locking während Splits und Merges. Bei hoher Parallelität kann Lock Contention Schreibvorgänge zum Flaschenhals machen.
Lösung: Latch-freie B-Trees (verwendet in modernen Datenbanken wie Microsoft SQL Server) oder MVCC (Multi-Version Concurrency Control).
Wann man B-Trees NICHT verwenden sollte
B-Trees sind ausgezeichnet für festplattenbasierte sortierte Daten, aber nicht immer optimal:
Schreib-intensive Workloads
Wenn Sie 100.000 Schreibvorgänge/Sekunde mit wenigen Lesevorgängen machen, übertreffen LSM-Trees B-Trees.
Vergleich:
| Metrik | B-Tree | LSM-Tree |
|---|---|---|
| Lesegeschwindigkeit | Schnell (O(log n)) | Langsamer (mehrere Ebenen) |
| Schreibgeschwindigkeit | Moderat (In-Place Updates) | Schnell (Append-only) |
| Speichereffizienz | 70-90% (Fragmentierung) | 90-95% (Compaction) |
| Anwendungsfall | Lese-intensives OLTP | Schreib-intensive Ingestion |
Beispiele:
- B-Tree: MySQL, PostgreSQL, SQLite
- LSM-Tree: RocksDB, Cassandra, LevelDB
In-Memory Datenbanken
Wenn Ihr gesamter Datensatz in den RAM passt, fügen B-Trees unnötige Komplexität hinzu. Hash-Indizes oder Skip Lists sind einfacher und schneller.
Vergleich:
| Metrik | B-Tree (In-Memory) | Hash Index | Skip List |
|---|---|---|---|
| Lookup | O(log n) | O(1) | O(log n) |
| Range Query | O(log n + k) | Nicht unterstützt | O(log n + k) |
| Speicher-Overhead | Hoch (interne Knoten) | Niedrig | Moderat |
| Anwendungsfall | Festplattenbasierter Speicher | Key-Value Caching | Redis Sorted Sets |
Beispiele:
- Hash Index: Memcached, Redis Hashes
- Skip List: Redis Sorted Sets
Analytische Workloads (OLAP)
Für grosse analytische Abfragen, die Millionen von Zeilen scannen, übertrifft spaltenorientierter Speicher (z.B. Parquet, ORC) B-Trees.
Vergleich:
| Metrik | B-Tree (Zeilenspeicher) | Spaltenorientierter Speicher |
|---|---|---|
| Point Query | Schnell | Langsam |
| Full Scan | Langsam (alle Spalten lesen) | Schnell (nur benötigte Spalten lesen) |
| Kompression | Niedrig | Hoch (spaltenweise Kompression) |
| Anwendungsfall | OLTP (Transaktionen) | OLAP (Analytik) |
Beispiele:
- Zeilenspeicher (B-Tree): MySQL, PostgreSQL
- Spaltenorientierter Speicher: Parquet (verwendet von Snowflake, BigQuery), ORC (verwendet von Hive)
Zusammenfassung: Warum B-Trees gewonnen haben
Nach über 50 Jahren bleiben B-Trees die dominierende Datenstruktur für Festplattenspeicher, weil sie:
- Festplatten-I/O minimieren: Hoher Fanout reduziert Baumhöhe
- Sich automatisch balancieren: Splits und Merges halten alle Blätter auf der gleichen Tiefe
- Range Queries unterstützen: Sortierte Schlüssel und Blatt-Verlinkungen ermöglichen effiziente Scans
- Auf jeder Festplatte funktionieren: Optimiert für HDDs (sequentielles I/O) und SSDs (Block-Level-Zugriff)
Kerninsight: B-Trees passen zu den Beschränkungen von Festplattenspeicher. Da die kleinste I/O-Einheit ein Block ist, packen B-Trees so viele Daten wie möglich in jeden Block. Diese einfache Idee—Fanout maximieren um Höhe zu minimieren—macht Datenbanken schnell.
Wann B-Trees verwenden:
- Festplattenbasierter Speicher (Datenbank-Indizes)
- Häufige Lesevorgänge und moderate Schreibvorgänge
- Range Queries auf sortierten Daten
- Allgemeine OLTP-Workloads
Wann Alternativen in Betracht ziehen:
- Schreib-intensive Workloads (LSM-Trees)
- In-Memory-Daten (Hash-Indizes, Skip Lists)
- Analytische Abfragen (spaltenorientierter Speicher)
Jedes Mal, wenn Sie Ihre Datenbank abfragen und ein Ergebnis in Millisekunden bekommen, danken Sie dem B-Tree.
Referenzen
Dieser Artikel basiert auf Kapitel 2 ("B-Tree Basics") von Database Internals: A Deep Dive into How Distributed Data Systems Work von Alex Petrov (O'Reilly, 2019).
Zusätzliche Ressourcen:
-
Bayer, R., & McCreight, E. (1972). "Organization and Maintenance of Large Ordered Indexes." Acta Informatica, 1(3), 173-189. https://doi.org/10.1007/BF00288683
-
Comer, D. (1979). "The Ubiquitous B-Tree." ACM Computing Surveys, 11(2), 121-137. https://doi.org/10.1145/356770.356776
-
Graefe, G. (2011). "Modern B-Tree Techniques." Foundations and Trends in Databases, 3(4), 203-402. https://doi.org/10.1561/1900000028
-
MySQL Documentation: "InnoDB B-Tree Indexes" https://dev.mysql.com/doc/refman/8.0/en/innodb-physical-structure.html
-
PostgreSQL Documentation: "B-Tree Indexes" https://www.postgresql.org/docs/current/btree.html
-
SQLite Documentation: "B-Tree Module" https://www.sqlite.org/btreemodule.html
Bücher:
-
Petrov, A. (2019). Database Internals: A Deep Dive into How Distributed Data Systems Work. O'Reilly Media. ISBN: 978-1492040347
-
Knuth, D. E. (1998). The Art of Computer Programming, Volume 3: Sorting and Searching (2nd Ed.). Addison-Wesley. ISBN: 978-0201896855
-
Graefe, G. (2011). Modern B-Tree Techniques. Now Publishers. ISBN: 978-1601984197
Brauchen Sie Hilfe bei der Datenbankoptimierung?
Bei MEMOTECH helfen wir Unternehmen, ihre Datenbank-Performance zu optimieren und skalierbare Architekturen zu implementieren.
Unsere Expertise:
- PostgreSQL & MySQL Optimierung
- Index-Strategien und Query-Tuning
- Datenbank-Migration und Modernisierung
- Performance-Analyse und Monitoring
Kostenlose Erstberatung - Lassen Sie uns über Ihre Datenbank-Herausforderungen sprechen.
Kontakt:
- Web: memotech.ch/contact
- E-Mail: contact@memotech.ch
- Termin: Kostenlose 30min Beratung buchen
MEMOTECH - IT-Consulting für KMU in der Schweiz

Mehmet Gökçe
Founder & CEO
Gründer von MEMOTECH mit über 26 Jahren Erfahrung. Spezialisiert auf E-Commerce-Lösungen und digitale Transformation für Schweizer KMU.